The article focussed on design principles of the PCA algorithm for dimensionality reduction and its implementation in Python from scratch.
Introduction
With the availability of high-performance CPUs and GPUs, it is pretty much possible to solve every regression, classification, clustering, and other related problems using machine learning and deep learning models. However, there are still various portions that cause performance bottlenecks while developing such models. A large number of features in the dataset are one of the major factors that affect both the training time as well as the accuracy of machine learning models.
The Curse of Dimensionality
In machine learning, “dimensionality” simply refers to the number of features (i.e. input variables) in your dataset.
While the performance of any machine learning model increases if we add additional features/dimensions, at some point a further insertion leads to performance degradation that is when the number of features is very large commensurate with the number of observations in your dataset, several linear algorithms strive hard to train efficient models. This is called the “Curse of Dimensionality”.
Dimensionality reduction is a set of techniques that studies how to shrivel the size of data while preserving the most important information and further eliminating the curse of dimensionality. It plays an important role in the performance of classification and clustering problems.

The various techniques used for dimensionality reduction include:
Principal Component Analysis (PCA)
Linear Discriminant Analysis (LDA)
Generalized Discriminant Analysis (GDA)
Multi-Dimension Scaling (MDS)
LLE
IsoMap
Autoencoders
This article is focused on the design principals of PCA and its implementation in python.
Principal Component Analysis(PCA)
Principal Component Analysis(PCA) is one of the most popular linear dimension reduction algorithms. It is a projection based method that transforms the data by projecting it onto a set of orthogonal(perpendicular) axes.
“PCA works on a condition that while the data in a higher-dimensional space is mapped to data in a lower dimension space, the variance or spread of the data in the lower dimensional space should be maximum.”
In the below figure the data has maximum variance along the red line in two-dimensional space.

Intuition
Let’s develop an intuitive understanding of PCA. Suppose, you wish to distinguish between different food items based on their nutritional content. Which variable will be a good choice to differentiate food items? If you choose a variable that varies a lot from one food item to another, you will be able to detach them properly. Your job will be much harder if the chosen variable is almost in the same quantity in food items. What if data doesn’t have a variable that segregates food items properly? We can create an artificial variable through a linear combination of original variables like New_Var = 4*Var1 - 4*Var2 + 5*Var3.
This is what essentially PCA does, it finds the best linear combinations of the original variables so that the variance or spread along the new variable is maximum.
Suppose we have to transform a 2-dimensional representation of data points to a one-dimensional representation. So we will try to find a straight line and project data points on them. (A straight line is one dimensional). There are many possibilities to select a straight line.

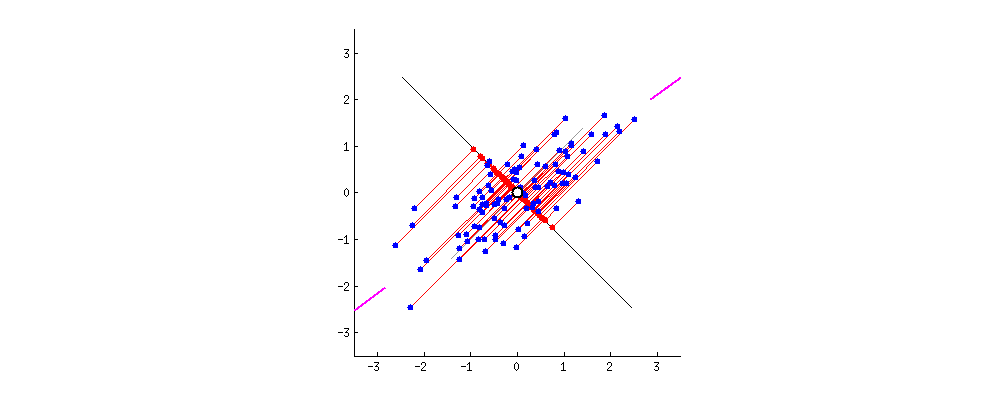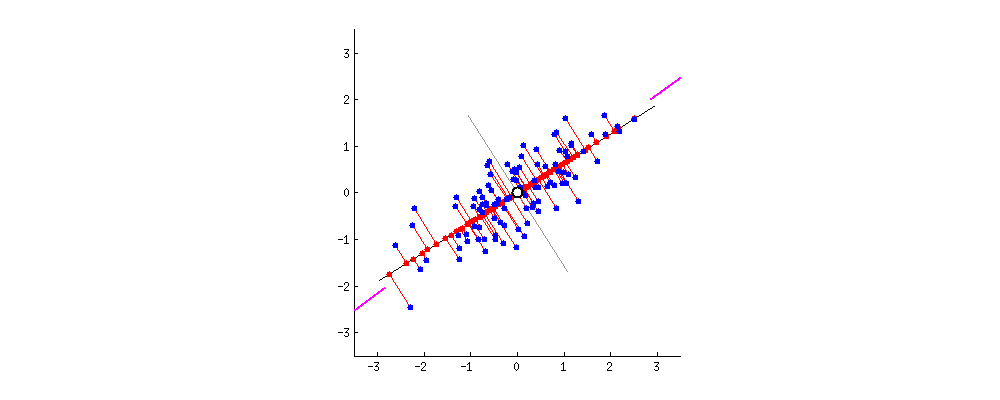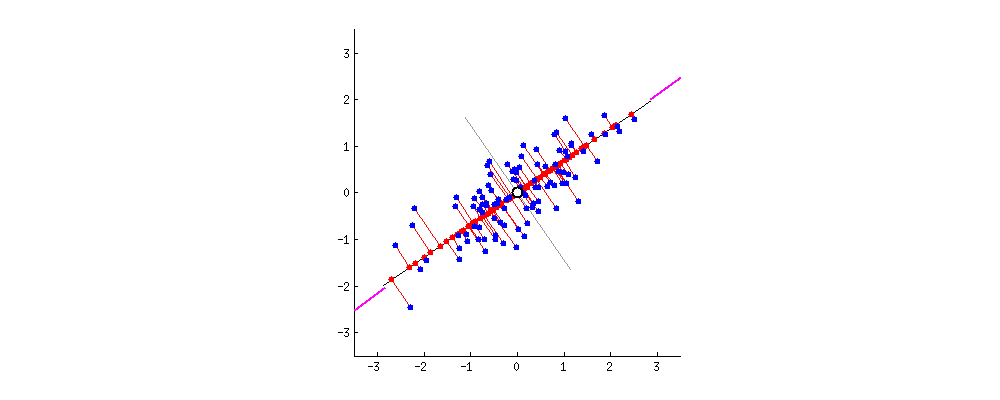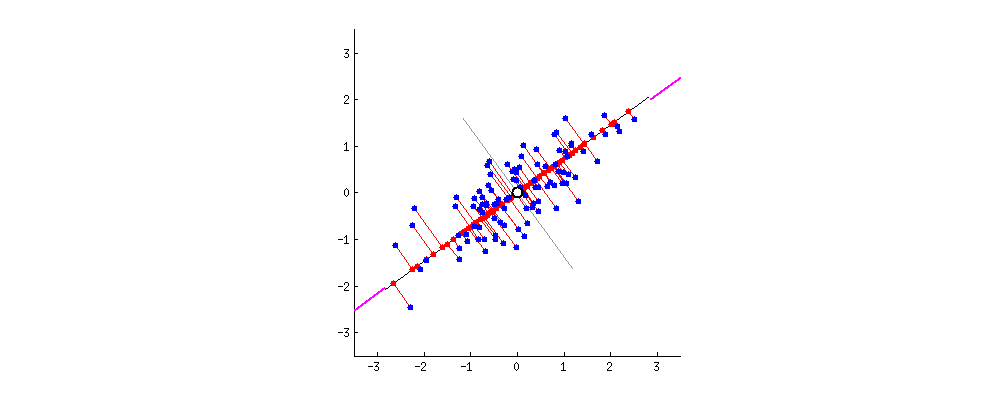
Say the magenta line will be our new dimension. If you see the red lines (connecting the projection of blue points on a magenta line) i.e. the perpendicular distance of each data point from the straight line is the projection error. The sum of the error of all data points will be the total projection error.
Our new data points will be the projections (red points) of those original blue data points. As we can see we have transformed 2-dimensional data points to one-dimensional data points by projection them on 1-dimensional space i.e. a straight line. That magenta straight line is called the principal axis. Since we are projecting to a single dimension, we have only one principal axis. We apply the same procedure to find the next principal axis from the residual variance. Apart from being the direction of maximum variance, the next principal axis must be orthogonal(perpendicular or Uncorrelated to each other,) to the other principal axes.
Once, we get all the principal axes, the dataset is projected onto these axes. The columns in the projected or transformed dataset are called principal components.
The principal components are essentially the linear combinations of the original variables, the weights vector in this combination is actually the eigenvector found which in turn satisfies the principle of least squares.
Luckily, thanks to linear algebra we don’t have to sweat much for PCA. Eigenvalue Decomposition and Singular Value Decomposition(SVD) from linear algebra are the two main procedures used in PCA to reduce dimensionality.
Eigenvalue Decomposition
Matrix Decomposition is a process in which a matrix is reduced to its constituent parts to simplify a range of more complex operations. Eigenvalue Decomposition is the most used matrix decomposition method which involves decomposing a square matrix(n*n) into a set of eigenvectors and eigenvalues.
Eigenvectors are unit vectors, which means that their length or magnitude is equal to 1.0. They are often referred to as right vectors, which simply means a column vector (as opposed to a row vector or a left vector).
Eigenvalues are coefficients applied to eigenvectors that give the vectors their length or magnitude. For example, a negative eigenvalue may reverse the direction of the eigenvector as part of scaling it.
Mathematically, A vector is an eigenvector of a matrix any n*n square matrix A if it satisfies the following equation:
A . v = 𝞴 . v
This is called the eigenvalue equation, where A is an n*n parent square matrix that we are decomposing, v is the eigenvector of the matrix, and 𝞴 represents the eigenvalue scalar.
In simpler words, the linear transformation of a vector v by A has the same effect of scaling the vector by factor 𝞴. Note that for m*n non-square matrix A with m ≠ n, A.v an m-D vector but 𝞴.vis an n-D vector, i.e., no eigenvalues and eigenvectors are defined. If you wanna diver deeper into mathematics check this out.

Multiplying these constituent matrices together, or combining the transformations represented by the matrices will result in the original matrix.
A decomposition operation does not result in a compression of the matrix; instead, it breaks it down into constituent parts to make certain operations on the matrix easier to perform. Like other matrix decomposition methods, Eigendecomposition is used as an element to simplify the calculation of other more complex matrix operations.
Singular Value Decomposition (SVD)
Singular value decomposition is a method of decomposing a matrix into three other matrices.

Mathematically Singular value decomposition is given by:

Where:
A is an m × n matrix
U is an m × n orthogonal matrix
S is an n × n diagonal matrix
V is an n × n orthogonal matrix
As shown, SVD produces three matrices U, S & V. U and V orthogonal matrices whose columns represent eigenvectors of AAT and ATA respectively. The matrix S is a diagonal matrix and diagonal values are called singular values. Each singular value is the square-root of the corresponding eigenvalue.
How does dimension reduction fit into these mathematical equations?
Well, once you have calculated eigenvalues and eigenvectors choose the important eigenvectors to form a set of principal axes.
Selection of EigenVectors
The importance of an eigenvector is measured by the percentage of total variance explained by the corresponding eigenvalue. Suppose V1 & V2 are two eigenvectors with 40% & 10% of total variance along with their directions respectively. If asked to pick one from these two eigenvectors, our choice would be V1 because it gives us more information about data.
All eigenvectors are arranged according to their eigenvalues in descending order. Now, we have to decide how many eigenvectors to retain and for that we need to discuss two methods Total variance explained and Scree Plot for that.
Total Variance Explained
Total Explained variance is used to measure the discrepancy between a model and actual data. It is the part of the model’s total variance that is explained by factors that are present.
Suppose, we have a vector of n eigenvalues(e0,..., en) sorted in descending order. Take the cumulative sum of eigenvalues at every index until the sum is greater than 95% of the total variance. Reject all eigenvalues and eigenvectors after that index.
Scree Plot
From the scree plot, we can read off the percentage of the variance in the data explained as we add principal components.
It shows the eigenvalues on the y-axis and the number of factors on the x-axis. It always displays a downward curve. The point where the slope of the curve is leveling off (the “elbow) indicates the number of factors.

For example in the scree plot shown above the sharp bend(elbow) is at 4. So, the number of principal axes should be 4.
Principal Component Analysis(PCA) in python from scratch
The example below defines a small 3×2 matrix, centers the data in the matrix, calculates the covariance matrix of the centered data, and then the eigenvalue decomposition of the covariance matrix. The eigenvectors and eigenvalues are taken as the principal components and singular values which are finally used to project the original data on the new axes.
from numpy import array
from numpy import mean
from numpy import cov
from numpy.linalg import eig
# define a small 3×2 matrix
matrix=array([[5, 6], [8, 10], [12, 18]])
print("original Matrix: ")
print(matrix)
# calculate the mean of each column
Mean_col=mean(matrix.T, axis=1)
print("Mean of each column: ")
print(Mean_col)
# center columns by subtracting column means
Centre_col=matrix-Mean_col
print("Covariance Matrix: ")
print(Centre_col)
# calculate covariance matrix of centered matrix
cov_matrix=cov(Centre_col.T)
print(cov_matrix)
# eigendecomposition of covariance matrix
values, vectors=eig(V)
print("Eigen vectors: ",vectors)
print("Eigen values: ",values)
# project data on the new axes
projected_data=e_vectors.T.dot(Centre_col.T)
print(projected_data.T)Output:
original Matrix: [[ 5 6] [ 8 10] [12 18]]
Covariance Matrix: [[12.33333333 21.33333333] [21.33333333 37.33333333]]
Eigen vectors: [[-0.86762506 -0.49721902] [ 0.49721902 -0.86762506]]
Eigen values: [ 0.10761573 49.55905094]
Projected data: [[ 0.24024879 6.28473039] [-0.37375033 1.32257309] [ 0.13350154 -7.60730348]]Conclusion
With all the effectiveness PCA provides, but if the number of variables is large, it becomes hard to interpret the principal components. PCA is most suitable when variables have a linear relationship among them. Also, PCA is susceptible to big outliers.
PCA is an old method and has been well researched. There are many extensions of basic PCA which address its shortcomings like robust PCA, kernel PCA, incremental PCA. Through this article, we developed a basic and intuitive understanding of PCA. We discussed a few important concepts related to its implementation.
Well, that’s all for this article hope you guys have enjoyed reading it and I’ll be glad if it is of any help. Feel free to share your comments/thoughts/feedback in the comment section.